Trigonometry Archives

Trigonometry Basics

Leave a Comment / Trigonometry / By zetutor.com

TRIGONOMETRY

Trigonometry is a branch of mathematics that connects with the angles and sides of a triangle. There are three major trigonometric functions. Sine(sin), Cosine(cos), Tangent(tan), and there are three minor trigonometric functions Cosent(csc), Secant(sec), and Cotangent(cot).

You can use this SOH, CAH, TOA to memorize the following

$sin\theta=\frac{Opposite}{Hypotenuse}$

cos\theta=\frac{Adjacent}{Hypotenuse}

tan\theta=\frac{Opposite}{Adjacent}

$csc\theta=\frac{Hypotenuse}{Opposite}$

sec\theta=\frac{Hypotenuse}{Adjacent}

cot\theta=\frac{Adjacent}{Opposite}

Major trigonometric and minor trigonometric are connected by the equations given below. Sin, Cos, Tan are the reciprocal of Csc, Sec, Cot respectively and vise versa.

$csc \theta =\frac{1}{sin \theta}$

$sec \theta =\frac{1}{cos \theta}$

$cot \theta =\frac{1}{tan \theta}$

Types Of Triangle

By Angle

1. Acute Triangle (less than 90 degrees)

2. Right Triangle (Equals to 90 degrees)

3. Obtuse Triangle (Greater than 90 degrees)

By Side

1. Equilateral Triangle

2. Isosceles Triangle

3. Scalene Triangle

Basic trigonometric basic function equations can be only used for right triangles. Sine law, Cosine law can be used for any types of triangles.

Pythagorean Theorem

The Pythagorean theorem is a fundamental mathematical equation that connects the sides and angles of a right triangle. It states that in a right triangle. The square of lengths of the hypotenuse is equals to the sum of squares of the length of the other two sides

a^2+b^2=c^2

c is the hypotenuse and a,b are the other two sides

Pythagorean theorem has various application in trigonometry and other part of mathematics. By combining trigonometric functions with Pythagorean theorem we can do the following things.

Trigonometric Ratios
Verifying trigonometric identities
Angle of elevations and depressions
Solving triangles

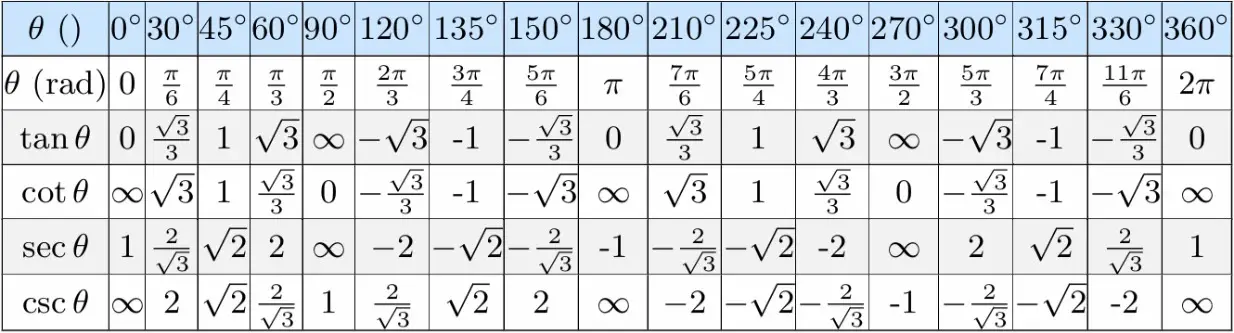
Ranges Of Trigonometric Functions

The ranges of the trigonometric functions depend on their equations and type of the functions and the nature of the unit circle.

1.SIne Function Range (SIN)

Range: [-1,1]

Sine functions can take values in between positive 1 and negative 1. Sine function represents the y coordinate of a unit circle.

2.Cosine Function Range (COS)

Range: [-1,1]

Cosine functions can take values in between positive 1 and negative 1. Cosine function represents the x coordinate of a unit circle.

3.Tangent Function Range (TAN)

Range: [ $-\infty,\infty$ ]

Tangent functions can take all real number values. That’s why the range is in between negative infinity and positive infinity. Tangent functions can be found when you divide the sine function by cosine function.

$tan \theta =\frac{sin\theta}{cos\theta}$

4. Cosecant Function Range (CSC)

Range: $\left ( -\infty,1 \right]\cup \left [1,\infty \right)$

Cosecant functions are the reciprocal of sine functions. Cosecant function can not take zero because cosecant zero is undefined.

5. Secant Function Range (SEC)

Range:

\left ( -\infty,1 \right]\cup \left [1,\infty \right)

Secant functions are the reciprocal of cosine functions. Secant function can not take zero because cosecant zero is undefined.

6. Cotangent Function Range (COT)

Range: [ $-\infty,\infty$ ]

Cotangent functions can take all real number values. That’s why the range is in between negative infinity and positive infinity. Cotangent functions can be found by dividing cosine function by sine function.

$cot \theta =\frac{cos\theta}{sin\theta}$

Fundamental Trigonometric Identities

Trigonometric identities are fundamental trigonometric equations that used to simplify expressions and solve equations.

Reciprocal identities

$csc \theta =\frac{1}{sin \theta}$

$sec \theta =\frac{1}{cos \theta}$

$cot \theta =\frac{1}{tan \theta}$

Quotient Identities

$tan \theta =\frac{sin\theta}{cos\theta}$

$cot \theta =\frac{cos\theta}{sin\theta}$

Pythagorean Identities

$sin^{2}\theta=1-cos^{2}\theta$

$sec^{2}\theta=1+tan^{2}\theta$

$csc^{2}\theta=1+cot^{2}\theta$

Even Identities

\sin (-\theta) =-sin\theta

\cos (-\theta) =cos\theta

\tan (-\theta) =-tan\theta

\csc (-\theta) =-csc\theta

\sec (-\theta) =sec\theta

\cot (-\theta) =-cot\theta

Sum And Difference Identities

sin (A + B) = sinA cosB + cosA sinB

sin (A – B) = sinA cosB – cosA sinB

cos (A + B) = cosA cosB – sinA sinB

cos (A – B) = cosA cosB + sinA sinB

tan(A+B) = $\frac{tanA+tanB}{1-tanAtanB}$

tan(A-B) = $\frac{tanA-tanB}{1+tanAtanB}$

Double Angle Identities

\sin (2\theta) =2sin(\theta)cos(\theta)

\cos (2\theta) =cos^{2}(\theta)-sin^{2}(\theta)

\cos (2\theta) =2cos^{2}(\theta)-1

\cos (2\theta) =1-2sin^{2}(\theta)

tan2\theta = \frac{2tan\theta}{1-tan^2\theta}

Half Angle Identities

\sin \frac{\theta }{2}=\pm\sqrt{\frac{1-cos\theta}{2}}

\cos \frac{\theta }{2}=\pm\sqrt{\frac{1+cos\theta}{2}}

\tan \frac{\theta }{2}=\pm\sqrt{\frac{1-cos\theta}{1+cos\theta}}

Trigonometric Function Table

Leave a Comment / Trigonometry / By zetutor.com

TRIGONOMETRIC FUNCTION TABLE

The representation of the trigonometric function angle value is the trigonometric function table. We have 3 major trigonometric functions Sine, Cosine, Tangent and 3 minor trigonometric functions Cosecant, Secant, Cotangent.

The table typically includes degrees and radians along with the corresponding angle value. The commonly used values are 0,30,45,60,90 degrees.

Trigonometric function table have various applications. Using this table we can solve the trigonometric function problem and we can find the unknown angles.

Radians and Degrees

2 Comments / Trigonometry / By zetutor.com

RADIANS AND DEGREES

Radians and Degrees are two units of measurement used to express angles.

The radian is denoted by the symbol rad and it is the system of units (SI) for angles.

The angle subtended when traveling a distance equal to the radius around a circle is known as the radian. The subtended angle after one complete rotation is equal to $2\pi$ radians.

The degree is denoted by ( $^{\circ}$ ). A full circle divided into 360 is called degrees. Each degree can be further divided in minutes(‘) and seconds(”).

1 $^{\circ}$

1’=60”

We can use the protractor to measure the angle

RADIANS TO DEGREE

$2\pi$ radians = 360 Degrees

$\pi$ radians = 180 Degrees

Equation

degrees = radians x $\left(\frac{180}{\pi}\right)$

Example: Convert $\left(\frac{\pi}{3}\right)$ to radians

Degrees = $\left(\frac{\pi}{3}\right)\times\left(\frac{180}{\pi}\right)$

= $\frac{180\pi}{3\pi}$

= 60 $^{\circ}$

Some common radians value in degrees

$\frac{\pi}{6}$ = 30 $^{\circ}$

$\frac{\pi}{4}$ = 45 $^{\circ}$

$\frac{\pi}{2}$ = 90 $^{\circ}$

$\frac{2\pi}{3}$ = 120 $^{\circ}$

$\frac{3\pi}{4}$ = 135 $^{\circ}$

$\frac{5\pi}{6}$ = 150 $^{\circ}$

${\pi}$ = 180 $^{\circ}$

$\frac{3\pi}{2}$ = 270 $^{\circ}$

${2\pi}$ = 360 $^{\circ}$

DEGREE TO RADIANS

360 Degrees = $2\pi$ radians

180 Degrees = $\pi$ radians

Equation

radians = degrees x $\left(\frac{\pi}{180}\right)$

Example: Convert 30 $^{\circ}$ to radians

Degrees = $30\times\left(\frac{\pi}{180}\right)$

= $\frac{30\pi}{180}$

Reduced by 30

= $\frac{\pi}{6}$

Trigonometric Identities

Leave a Comment / Trigonometry / By zetutor.com

TRIGONOMETRIC IDENTITIES

Trigonometric identities serve as essential mathematical tools that establish connections between different trigonometric functions. These relationships are universally valid, holding true for all values within the specified domains. Trigonometric identities play a pivotal role in simplifying complex trigonometric expressions, proving mathematical assertions, and solving equations involving trigonometric functions.

DOUBLE ANGLE TRIGONOMETRIC IDENTITIES

RECIPROCAL IDENTITIES

Reciprocal identities expresses a trigonometric function in a reciprocal form. Reciprocal identities establish a relationship between three trigonometric functions sine, cosine, tangent and their reciprocals cosecant, secant, tangent.

1. Cosecant Reciprocal Identities

$csc \theta =\frac{1}{sin \theta}$

2. Secant Reciprocal Identities

$sec \theta =\frac{1}{cos \theta}$

3. Cotangent Reciprocal Identities

$cot \theta =\frac{1}{tan \theta}$

QUOTITENT IDENTITIES

Quotient identities expresses a one trigonometric function as a quotient of two others. There are two primary quotient identities

1. Quotient identity for tangent

$tan \theta =\frac{sin\theta}{cos\theta}$

This identity is very useful to make a connection with the three major trigonometric functions sine, cosine, tangent

2. Reciprocal identity for cotangent

$cot \theta =\frac{cos\theta}{sin\theta}$

This identity is very useful to make a connection with the three minor trigonometric functions sine, cosine, tangent

PYTHAGOREAN IDENTITIES

Pythagorean identities are set of three trigonometric identities that are derived from the Pythagorean theorem. These identities involve 3 major trigonometric functions sine, cosine and tangent.

1. Sine Squared Identity $sin^{2}\theta+cos^{2}\theta=1$

sin^{2}\theta=1-cos^{2}\theta

$cos^{2}\theta=1-sin^{2}\theta$

2. Secant Squared Identity $sec^{2}\theta=1+tan^{2}\theta$

$sec^{2}\theta-tan^{2}\theta=1$

$tan^{2}\theta=sec^{2}\theta-1$

3. Cosecant Squared Identity $csc^{2}\theta=1+cot^{2}\theta$

$csc^{2}\theta-cot^{2}\theta=1$

$cot^{2}\theta=csc^{2}\theta-1$

SUM AND DIFFERENCE TRIGONOMETRIC IDENTITIES

The sum and difference trigonometric identities are formulas that express two angles as a form of sum or difference.

There are six sum and difference formulas. We can use the sum and difference formulas for Sine, Cosine and Tangent functions.

These trigonometric identities are used to find some unknown angles and simplifying expressions and solving trigonometric equations.

Here are the list of sum and difference formula

sin (A + B) = sinA cosB + cosA sinB
sin (A – B) = sinA cosB – cosA sinB
cos (A + B) = cosA cosB – sinA sinB
cos (A – B) = cosA cosB + sinA sinB
tan(A+B) = $\frac{tanA+tanB}{1-tanAtanB}$
tan(A-B) = $\frac{tanA-tanB}{1+tanAtanB}$

EVEN TRIGONOMETRIC IDENTITIES

Even trigonometric functions satisfy the following condition f(x) = f(-x) for all x values. Even function applied to angle and its negative angle will give you the same results.

Major trigonometric functions even identities

\sin (-\theta) =-sin\theta

\cos (-\theta) =cos\theta

\tan (-\theta) =-tan\theta

Minor trigonometric functions even identities

\csc (-\theta) =-csc\theta

\sec (-\theta) =sec\theta

\cot (-\theta) =-cot\theta

Even identities are useful in simplifying expressions and providing trigonometric identities relationships and solving trigonometric equations.

DOUBLE ANGLE TRIGONOMETRIC IDENTITIES

Double angle trigonometric identities express trigonometric functions of twice an angles in terms of the trigonometric functions of that angle. Here are the double angle trigonometric identities

Sine Double Angle Identity

\sin (2\theta) =2sin(\theta)cos(\theta)

Cosine Double Angle Identity

\cos (2\theta) =cos^{2}(\theta)-sin^{2}(\theta)

\cos (2\theta) =2cos^{2}(\theta)-1

\cos (2\theta) =1-2sin^{2}(\theta)

Tangent Double Angle Identity

tan2\theta = \frac{2tan\theta}{1-tan^2\theta}

We can derive these double angle identities from various trigonometric identities and formula such as the sum and difference identities and these identities are applicable for all values of $\theta$ .

There is also half angle trigonometric identities which expresses trigonometric functions in half angle in terms of the original trigonometric functions. These identities are obtained by rearranging the double angle identities.

HALF ANGLE TRIGONOMETRIC IDENTITIES

Half angle trigonometic identities are obtained by rearranging the double angle identities.

Sine half angle identity

$\sin \frac{\theta }{2}=\pm\sqrt{\frac{1-cos\theta}{2}}$

Positive or negative square root depends sign on the quadrant in which $\frac{\theta}{2}$ lies.

Cosine half angle identity

\cos \frac{\theta }{2}=\pm\sqrt{\frac{1+cos\theta}{2}}

Positive or negative square root depends sign on the quadrant in which

\frac{\theta}{2}

lies.

Tangent half angle identity

\tan \frac{\theta }{2}=\pm\sqrt{\frac{1-cos\theta}{1+cos\theta}}

Positive or negative square root depends sign on the quadrant in which

\frac{\theta}{2}

lies.

These identities are obtained by applying the double-angle trigonometric identities and solving for the half-angle expressions. They are very helpful for simplifying trigonometric expressions involving half angles.