FACTORING QUADRATIC EQUATIONS
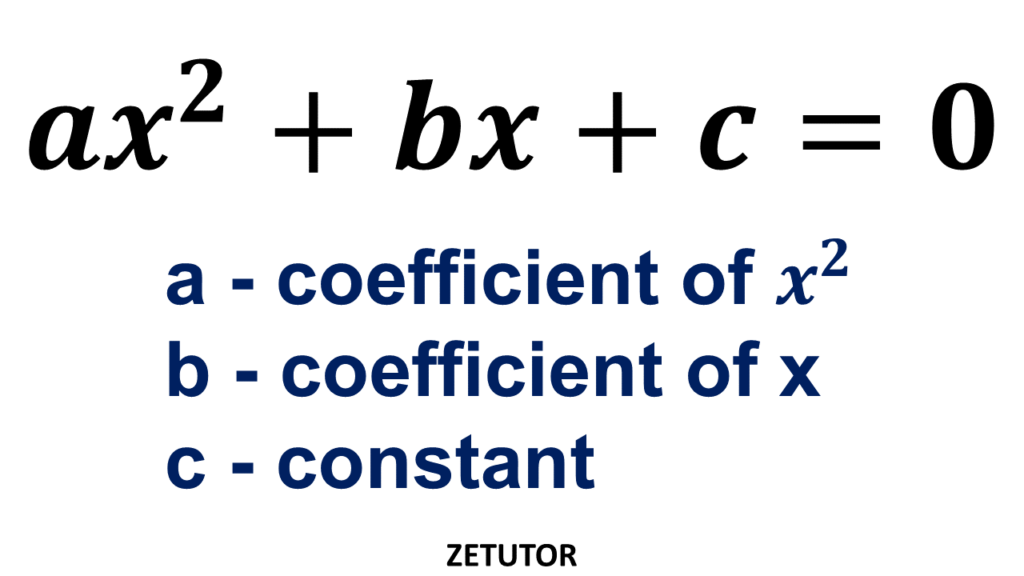
Quadratic equation is a second degree polynomial function with the single variable. The standard form quadratic function is given by
ax^2+bx+c=0, where x represents the variable and a is the coefficent of x^2, b is the coefficient of x and c is a constant. a,b,c can take all real numbers. a is not equal to zero because if a is equals to zero then the second degree polynomial won’t exist
The solution of the quadratic equation can be found using the quadratic formula
x=\frac{-b\pm \sqrt{b^{^{2}}-4ac}}{2a}
In the quadratic formula discriminant is an important one. The term inside the square root b^2-4ac is called discriminant. Discriminant plays an important rule to determine the nature of the solutions. The three cases are given below
1. b^2-4ac>0 : This means discriminant is positive because greater than zero indicates the positive numbers. When the discriminant is positive, the quadratic equation have two distinct real solutions/roots/zeros. If you draw the graph of positive discriminant quadratic function the graph will intersect the x axis at two distinct points.
2. b^2-4ac=0 : This means discriminant equals to zero. When the discriminant is zero, there is exactly one real solution. These types of quadratic equations are perfect square trinomial. If you draw the graph of the discriminant zero quadratic function, it will intersect the x axis at exactly one point. This is a single point of intersection.
3. b^2-4ac<0 : This means discriminant is negative because less than zero indicates the negative numbers. When the discriminant is negative, the quadratic equation have two complex solution which involves imaginary numbers. And the graph won’t intersect the x axis at any point.
Factoring quadratic equations is a method of expressing them as a product of two linear functions.
Example: x^2+5x+6 =(x+2)(x+3)
(x+2) and (x+3) are the factors of x^2+5x+6
Factoring Quadratics Equations Methods
1. Cross Method / Product Sum Method
2. Algebraic Identities
3. Quadratic Formula
Cross Method / Product Sum Method
Consider a quadratic equation x^2+6x+8 = 0
1. Find two numbers m and n such that m x n = 8 (constant), m+n=6 (middle term)
2. According to the first step m=4, n=2
3. Rewrite the middle term using m and n
So the final answer is x^2+6x+8 = (x+4)(x+2)
Algebraic Identities
Algebraic identities are expressions that are valid for all values of the variable. There are different algebraic identities. Here are some of them.
1. Factorizing a perfect square trinomial
a^2+2ab+b^2=(a+b)^2
a^2-2ab+b^2=(a-b)^2
Example x^2-10x+25=(x-5)^2
2. Factorizing the difference of squares
a^2-b^2=(a+b)(a-b)
Example x^2-4^2=(x+4)(x-4)
3. Factorizing the sum of cubes
a^3+b^3=(a+b)(a^2-ab+b^2)
Quadratic Formula
The quadratic formula is a direct method of finding the solution of a quadratic function. Above mentioned cross method or algebraic identities can not be used for all quadratic functions but the quadratic formula can be used for all quadratic functions. The quadratic formula is given below
x=\frac{-b\pm \sqrt{b^{^{2}}-4ac}}{2a}Where,
x = unknown variable
a = coefficient of x^2, b – coefficient of x, c – constant
\pm = This means there is a possibility for two solutions. One with a Plus sign and another with a Minus sign.
Follow these steps to use the quadratic formula
1. Find the a, b, c values from the quadratic equation
2. Plugin the values in the quadratic formula
3. Simplify the equation and find the solutions.
Example: 2x^2-5x+2
a=2, b=-5, c=2
x=\frac{-(-5)\pm \sqrt{(-5)^{^{2}}-4(2)(2)}}{2(2)}
x=\frac{5\pm \sqrt{25-16}}{4}x=\frac{5\pm \sqrt{9}}{4}
x=\frac{5\pm 3}{4}Plus x=\frac{5+3}{4}
x=\frac{8}{4}
x=2
Minus x=\frac{5-3}{4}
x=\frac{2}{4}
x=\frac{1}{2}
Not all quadratic equations are factorable over the real numbers. In this case quadratic formula is the only way to find the solution or factors.
Applications Of Factoring Quadratic Equation
1. Solving Equations
Factoring is one of the easiest and most effective ways to solve a quadratic equation.
2. Quadratic Graph Analyze
Factoring is used to find the x intercepts or roots and y intercepts
3. Algebraic Simplification
Most of the time algebraic expressions or equations are complex, factoring can be used to simplify the algebraic equations.
