FUNCTIONS
A function is a relation between a set of inputs (x values) and a set of possible outputs (y values).
A function is like a machine. If you give a input to a function it will give you an an output.
F(x) is the function notation. F(x) is not f times x, you need to read it as function of x
Domain : All the inputs are called domain
Range: All the outputs are called range.
Example: let’s take f(x) = x+3 is a function.
Let’s give an input x=6, so x=6 one of the domain. If you give input 6 you will get an output f(x) = 6+3=9. So f(x)= 9 is one of the range value.
IDENTIFYING FUNCTIONS
Not all the equations are functions. There are some methods used to identify the functions
1. Vertical Line Test
2. Mapping Of Elements
VERTICAL LINE TEST
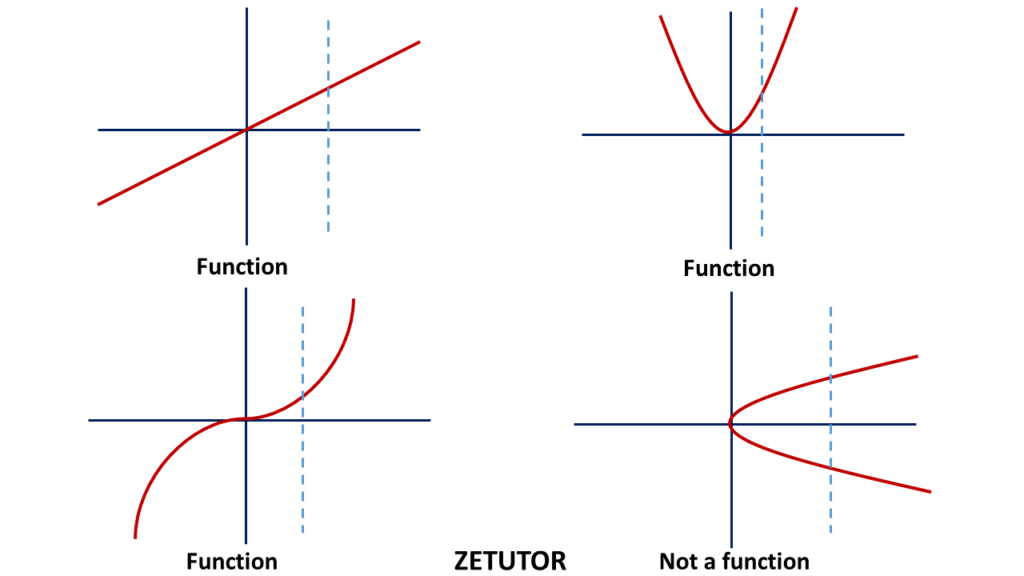
For a relation to be function each input value ( x value) must be associated with only one output value (y value).
First draw the graph of a given function and draw a vertical line and moving it across the graph.
If at any point the vertical line intersects the graph at more than one point, the relation is not a function.
A relation is a function if the vertical line intersects the graph at most one point for each potential x-value.
MAPPING OF ELEMENTS
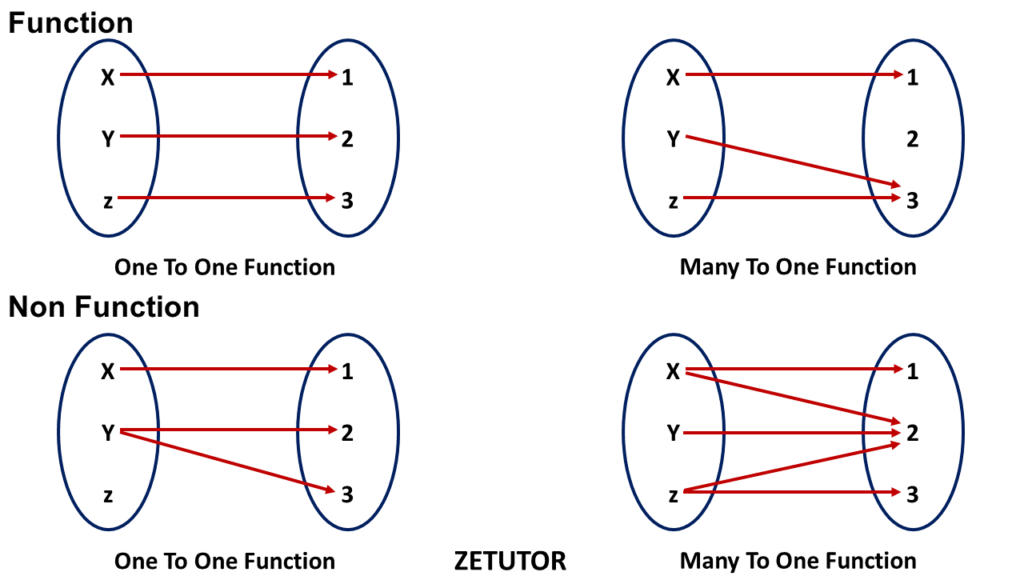
Let’s take input on one side and output on another side. One To One and Many To One is a function.
One To Many and Many To Many is not a function.
One To One Function
This is a function between two sets. Let’s take the two sets as A and B. If every element in A connects with a distinct element of B, then it is a One To One function. Set A is domain and set B is a codomain
Definition of a function also can be expressed using domain and codomain. When every element of domain set connects with a distinctive element of codomain set it will be considered as one to one function. This is also called as injective function.
Many To One Function
Types of Functions
Types of function can be represented in many ways. Here is the list of common list.
1. Polynomial Function – Linear Function, Quadratic Function, Cubic Function, Quartic Function, Quintic Function
2. Trigonometric Function
3. Exponential Function
4. Logarithmic Function
5. Rational Function
6. Modulus Function
7. Inverse Function
8. Greatest Integer Function
Polynomial Function
A polynomial function is a algebraic function. Polynomial function contain variables of varying degrees, coefficients and constants. The standard of polynomial function is given below
f(x)=a_{n}x^{^{n}}+a_{n-1}x^{^{n-1}}+a_{2}x^{^{2}}+a_{1}x++a_{0}Where,
n is the degree of the polynomial and non negative integer.
a_{n} is the leading coefficient
a_{n}, a_{n-1}, a_{0} are the coefficient of the variable
Degree is the highest exponent of a given polynomial. Coefficients can be real number or complex number.
Trigonometric Function
Trigonometric functions are mainly used for right triangles. It creates a connection between the side and angle of a triangle. There are 3 major trigonometric functions sine(sin), cosine(cos) and tangent(tan) and there are 3 minor trigonometric function cosecant(csc), secant(sec), cotangent(cot).
Exponential Function
y=ab^x is the general form of an exponential function. where a, b are constants and x is an independent variable. y=e^x is also considered as an exponential function but we have special name for that it’s called natural exponents. When a exponential function increases it is called exponential growth and when it decreases it is called exponential decay.
Logarithmic Function
Logarithmic functions are the inverse of exponential function. Logarithmic functions are denoted by \log_{a}x. Here a is the base and x is the argument. We can classify the logarithm mainly into two types
Common Logarithm : These type of logarithm has a base of 10 and it is denoted by log x
Natural Logarithm : When the base is e (Euler’s number) it is called natural logarithm. Euler’s number is an irrational constant approximately equals to 2.71828…
Rational Function
y is a rational function and f(x), g(x) are polynomials. g(x) is not equal to 0 because when the denominator equals to zero the whole rational function will become undefined. Rational functions are mainly used to describe the ratios and proportions.
