LINEAR FUNCTION
Linear function has a linear relationship between x variable (independent variable) and y variable (dependent variable). This implies a constant rate of change.
For every unit increase in the x variable, the dependent variable y changes with a constant amount. The The general form of linear function is given by
f(x) = mx + b
where,
x input or independent variable
f(x) output or dependent variable
m is the slope of the line
b is the y intercept
SLOPE INTERCEPT FORM
The slope intercept form represents the equation of a straight line. The slope intercept form is given by
y = mx + b
where,
y – Dependent variable
x – Independent variable
m – Slope
b – Y Intercept (y-axis crossing point)
Example: y = 5x + 7 is a slope intercept form
slope = 5, y intercept = 7
SLOPE
The slope is the rate of change or simply it represents the steepness of the line. The slope is the coefficient of the independent variable x or the number in front of the x. The slope indicates the y changes for a unit change in x.
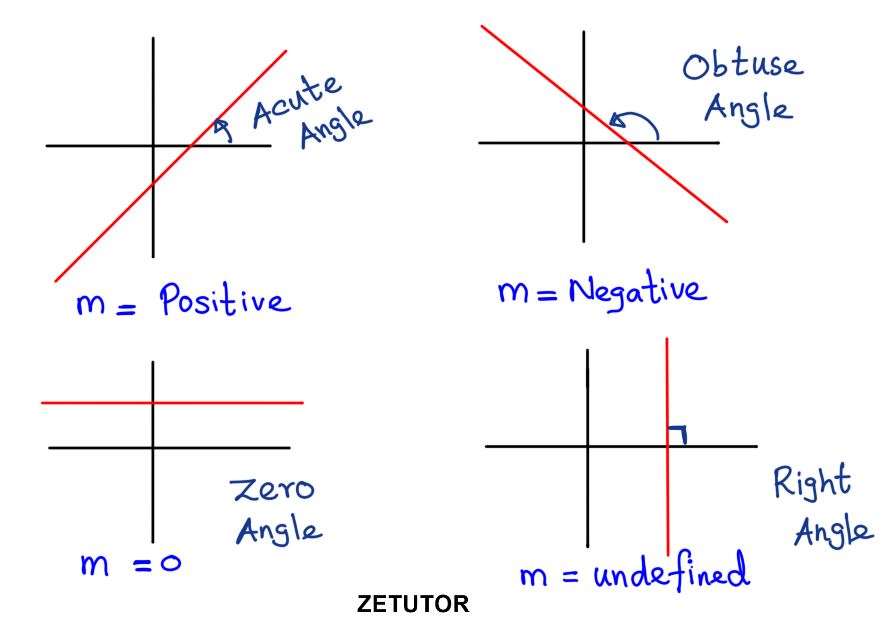
According to the sign of the slope, the line’s angle with horizontal will change
m positive – Line makes an acute angle with horizontal
m negative – Line makes an obtuse angle with horizontal
m zero – Horizontal line
m undefined -Vertical line
The slope is used in mathematics and physics. In physics slope of a position vs time, graph is equal to velocity. In a velocity vs time graph, the slope is equal to acceleration.
SLOPE FORMULA
slope =\frac{rise}{run}
slope =\frac{Change in y}{Change in x}
slope =\frac{y_{2}-y_{1}}{x_{2}-x_{1}}
where
(x_{1}, x_{1}) and (x_{2},y_{2}) two coordinates
Check the video for examples
Y INTERCEPT
This is the point where the graph crosses the y axis. You can find y intercept by making x=0 in the y=mx+b equation. Always x coordinate of y intercept equals to zero. So the y intercept coordinate will be (0,b)
POINT SLOPE FORM EQUATION
Point Slope form is a another way to express the linear equations but it’s particularly used when you know the coordinates of a specific point on the line and the slope of the line. The point slope form equation is given by
y-y_{1}=m(x-x_{1})(x_{1},y_{1}) known coordinate
m is the slope of the line
Plugin the known coordinate and slope in the point slope form equation and after simplifying that we are able to change point slope form equation to slope intercept form y=mx+b
EQUATION OF LINES
Point slope formy-y_{1}=m(x-x_{1})
Slope intercept form y = mx + b
Horizontal line x=0
Vertical line y=0
General form Ax+By+C=0
PARALLEL LINES
If two lines are not intersect and maintains a constant distance between each of them they are parallel line. Parallel lines have the same slope. For example if you consider the two parallel lines only the y intercept is different. So the two equations will be like this. y=mx+b and y=mx+c where b and c are the y intercepts
Parallel lines run side by side do not converge or diverge.
Example: Line y=3x+5 and y=3x+7 are parallel because both has same slope 3
PERPENDICULAR LINES
When two lines intersect with 90 degrees angle(right angle) they are perpendicular lines. The slopes of perpendicular lines are negative reciprocal of each other.
m_{1}\times ,m_{2}=-1If the slope of the line is m, the slope of the perpendicular line will be -1/m
Example: y=2x+4 and y=\frac{1}{2}x+8 are perpendicular because 2\times\frac{1}{2}=-1
EPILOGUE
Linear equations have many applications in physics, engineering, economics and biology. They provide a simple yet powerful tool for modeling and analyzing relationships between variables with a constant rate of change. The graphical representation of linear functions is straight line which is very helpful in both theoretical and practical contexts.
